Find the Quadratic Polynomial Which Best Fits the Data Points

Y 0218x3 2239x2 6084x 300915. Generate 10 points equally spaced along a sine curve in the interval 04pi.

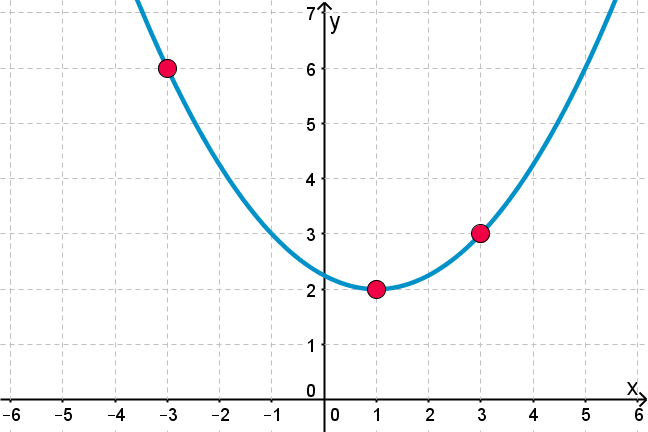
A Quadratic Function Through Three Points

Hence the need to work in the least-squares setting.

. Find the best-fit quadratic polynomial to the CO2 data. A d x d The goal is to minimize the sum of the squares of the vertical distances between the curve and the points. The user should be able to choose the degree d of polynomial and the vector X of evaluation points.

Print the c values as you will need these to compare to part b. Is linear in the variables a b and c which are the undetermined coefficients of the quadratic equation in x. We can be sure that such a function exists.

Y 0218 43 2239 42 6084 4 300915 2547. Show activity on this post. Note that in this system the x i and y j are constants and we are trying to solve for c 0 and c 1.

By substituting the data points. However it will be badly behaved because in between the points it will go haywire so the estimates will be worthless. Stack Exchange network consists of 179 QA communities including Stack Overflow the largest most trusted online community for developers to learn share their knowledge and build their careers.

C 0 c 1 x 1 y 1 c 0 c 1 x 2 y 2 c 0 c 1 x n y n. Y ax² bx c. Y 3 a x 3 2 b x 3 c.

Evaluate the polynomial on a finer grid and plot the results. Y1 polyval px1. The goal of this problem is to find the polynomial of order 5 that gives the best least square fit to the data.

Plus the exploits see which is the standard form in equation for a quadratic or specifically a problem. Figure plot xy o hold on plot x1y1 hold off. Set up the matrix X Create the vector z Create the matrix S Find the cholesky decomposition of S and store it in U Solve the triangular system UTW z using the backslash command.

So the three equations are. In addition it generates a scatter plot that depicts the curve of best fit. Find the quadratic polynomial that best.

In linear regression the model specification is that the dependent variable y is a linear combination of the parameters but need not be linear in the independent. Since a b and c are bound in a linear relationship you can use the least squares method to find the best values of a b and c. Y c 0 c 1 x c 2 x 2 y c_0c_1xc_2x2 y c 0 c 1 x c 2 x 2.

For the relation between two variables Polynomial Regression Calculator finds the polynomial function that best fits a given set of data points. For example suppose x 4. Plot the data together with the polynomial fit.

For n 2 there will be a solution but in the overdetermined case there almost always fails to be one. Numerical Mathematics and Computing 7th Edition Edit edition Solutions for Chapter 91 Problem 19E. We can also use this equation to calculate the expected value of y based on the value of x.

Use polyfit to fit a 7th-degree polynomial to the points. Helpful 1 The best fit will be a 9th order polynomial - it will go through each point exactly. Fit the data using a polynomial function where Mis the order of the polynomial Is higher value of Mbetter.

A 0 x 0 A 1 x 1 A 2 x 2. How to find the quadratic equation of best fit for five points in the shape of a parabola. So were given three data points by the problem and we have to try to find out.

I tried some twists and visualizations and think you datapoints cant be fit by such polinome. Coefficients w 0w Mare collectively denoted by vectorw It is a nonlinear function of x but a linear function of the unknown parameters w Have important properties and are called Linear Models yxw. For a given data set of xy pairs a polynomial regression of this kind can be generated.

SOLVEDFind the best least squares fit to the data in Exercise 5 by a quadratic polynomial. Y f x a x 2 b x c. A d to make the following equation fit the data points as closely as possible.

A Follow Example 1 to find the coefficients of the best polynomial fit of order 5 make sure you appropriately modify the matrix X. Y 2 a x 2 2 b x 2 c. Be the least squares regression quadratic polynomial of the given set of data points.

So like Wayne said you need to decide on an order. Quadratic formula fits through all of the points in this from this general equation y equals X squared. But its a terrible fit.

Y 1 a x 1 2 b x 1 c. Im not sure if I understood your question correctly but this may be what you want. Make a function called leastSquaresm which given some data points de ned by the vectors x and y will nd and evaluate the least-squares polynomial.

Make sure you define your vector q so. You can use the quadratic regression calculator in three simple steps. I need to find the polynomial function of degree 29 that exactly fits thirty data points.

Had 1000 data pairs very useful to show that despite a seemingly very high fit correlation as one fits subsets toward the higher end one quickly realizes that rather than 10x23x this site found 10x2x the true fit. X1 linspace 04pi. In this regression method the choice of degree and the evaluation of the fits quality depend on judgments that are left to the user.

In least squares regression the aim is to find the values of a b and c that minimize the squared vertical distances between each data. If you enter 1 for degree value so the regression would be linear. Solve the triangular system Uc w using the backslash command Compute the.

This Quadratic Regression Calculator quickly and simply calculates the equation of the quadratic regression function and the associated correlation coefficient. Plot the points x-1012 for your function and sketch the graph. The rst line should declare that the m- le is a function with four inputs and one.

Why you sure of this. In which represent coefficients created by a mathematical procedure described in detail here. LinearModelFit data x 1 - x x IncludeConstantBasis - False FittedModel 564463 1-xx This quadratic curve intersects the x -axis at x 0 and x 1 as desired.

You can enter the data into Excel and make a trendline which includes the option of using a quadratic or other polynomial fit. Checking sites analysis vs LibreCalc. Subtracting the first to the second and the second from the third already eliminates c and your are left with two linear equations for two unknowns.

The expected value of y would be. 0 2 1 3 2 2 5 2 3 4 02 1dfrac 3 2 2dfrac 5 2 34 0 2 1 2 3 2 2 5 3 4 into the above quadratic polynomial we obtain the following system of linear. But also the fact that it looks like a parabola to you doesnt necessarily mean that that is the most appropriate form.

Given a collection of points left x_ 1 y_ 1.

Least Squares Quadratic Example Youtube

Sequences And Series Analysis Find Quadratic Polynomial That Approximates Unit Circle Near Point 0 1 Osculating Parabola Mathematics Stack Exchange

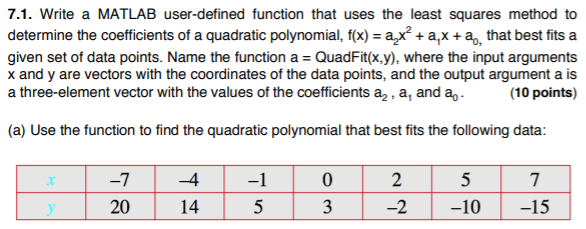
Solved 7 1 Write A Matlab User Defined Function That Uses Chegg Com